State-Space Models & Kalman Filter
I design and implement state-space models in R, from simple local-level structures to multivariate dynamic systems. Workflows include parameter estimation, inference, and publication-quality plots for filtering, smoothing, and forecasting.
Model classes & components: local level, local linear trend (slope), seasonal (additive/multiplicative), regression with time-varying coefficients (dynamic regression), ARIMA equivalence via innovations state-space, multivariate DLMs, intervention/outlier effects, missing-data handling, and constraints (e.g., positivity).
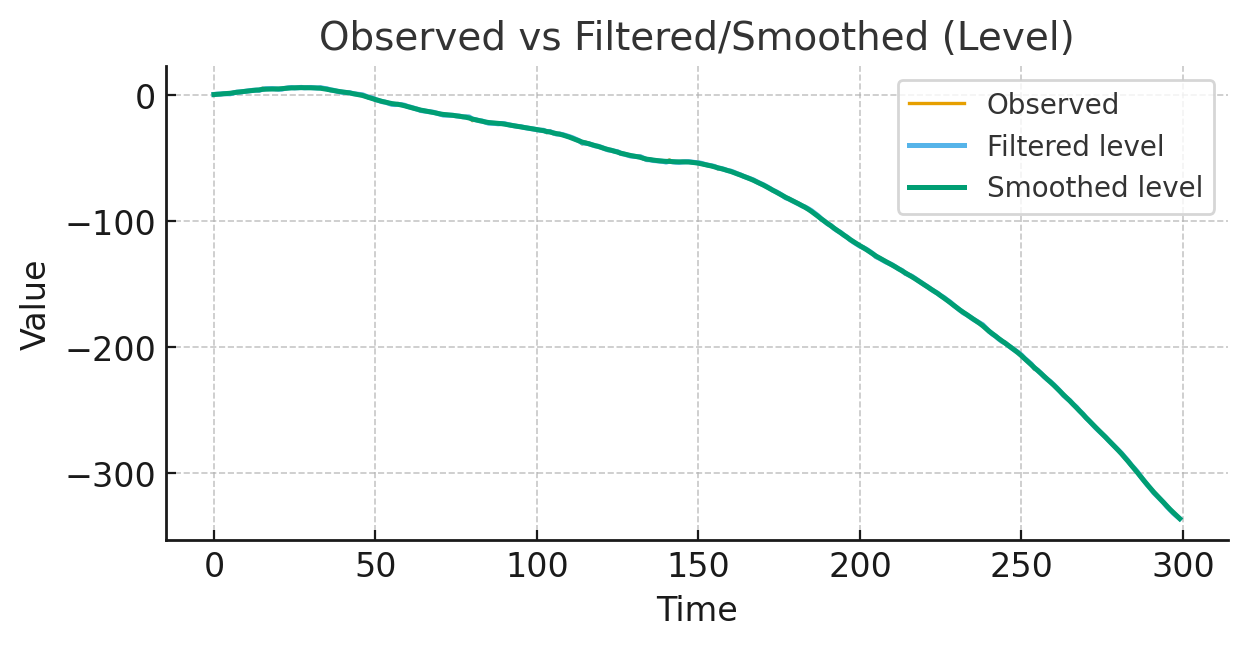
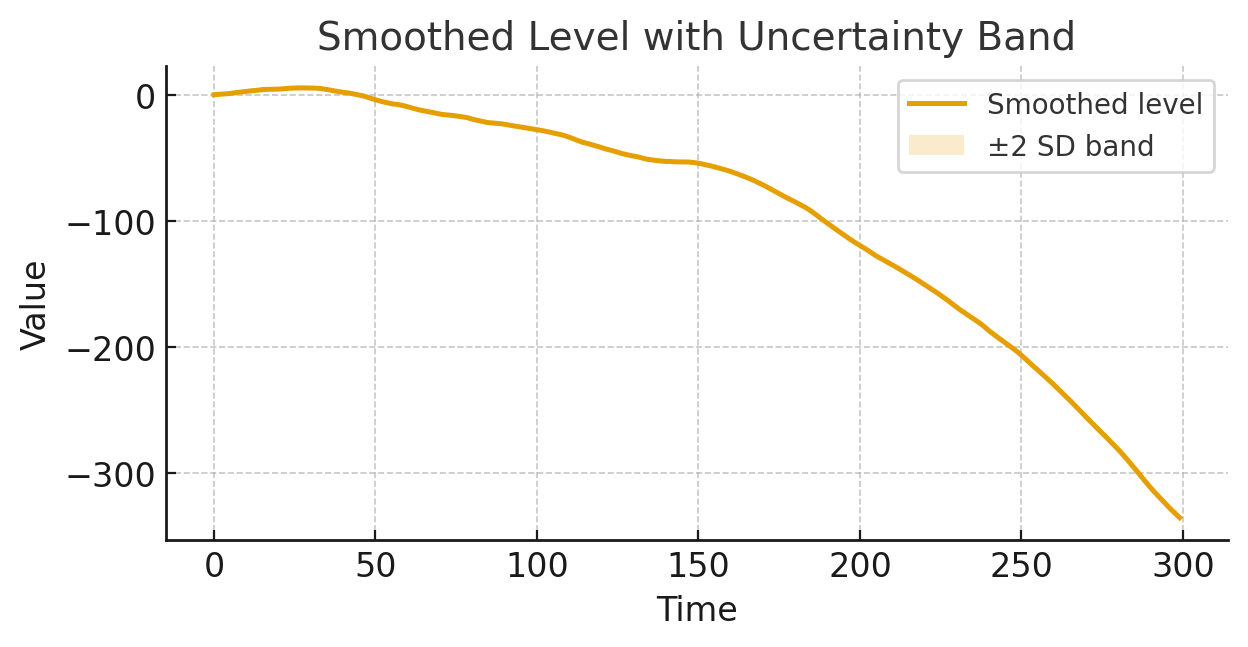
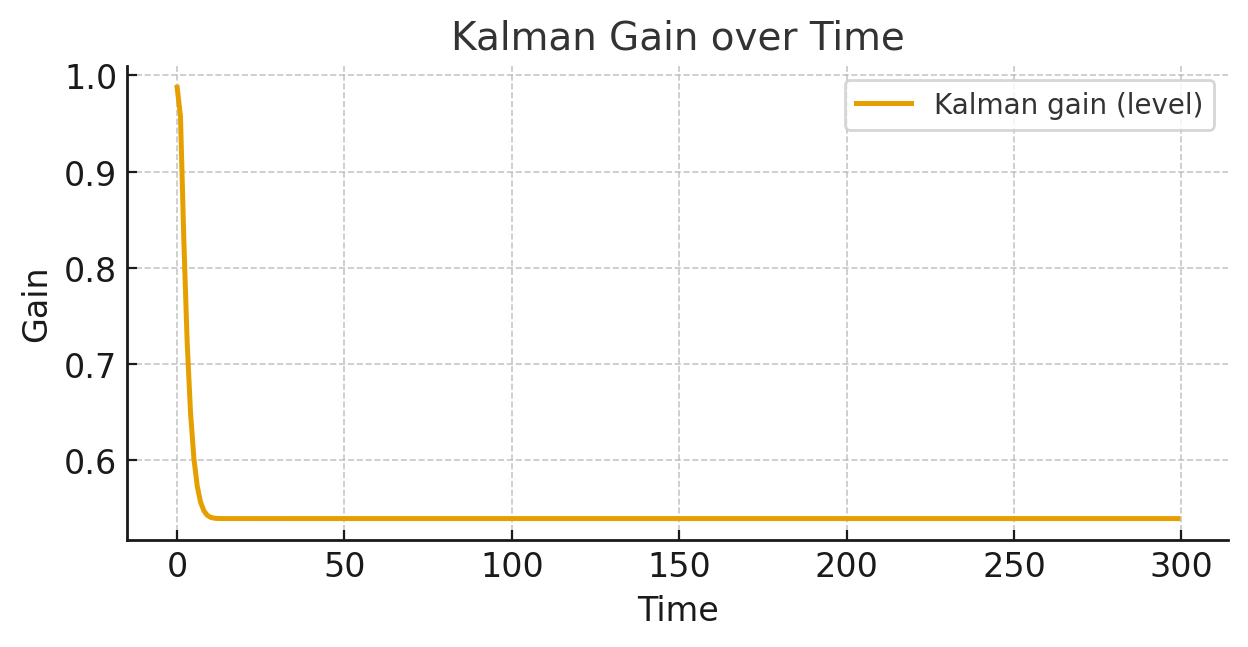
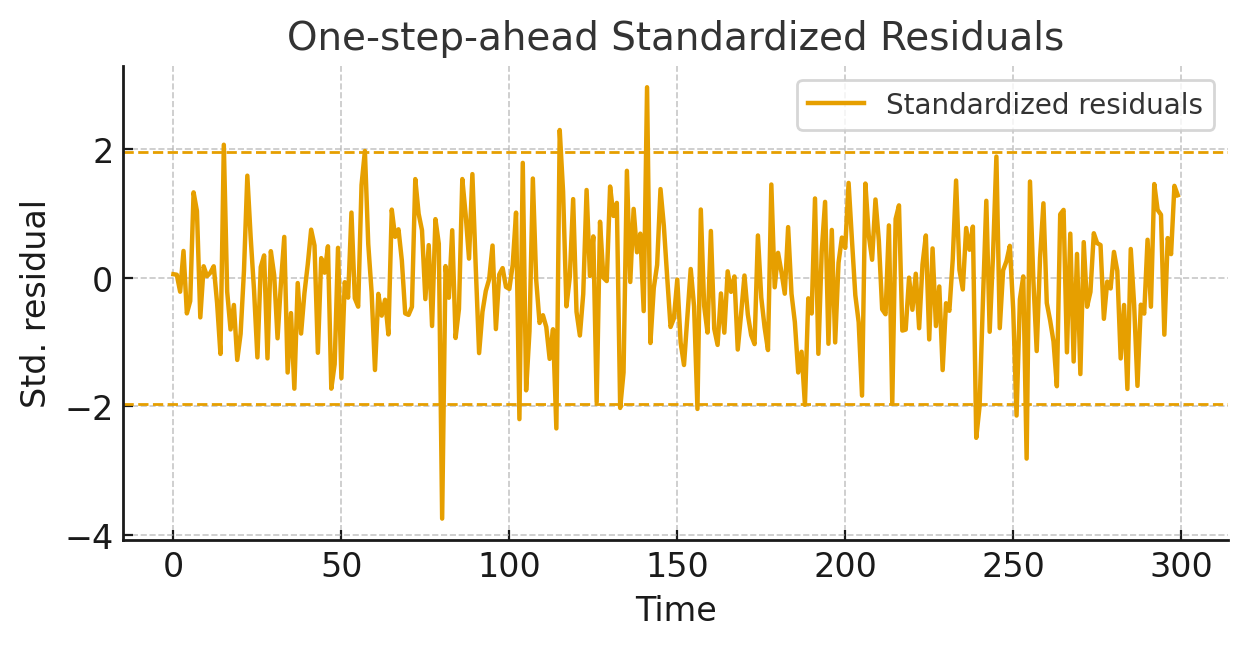
Estimation & inference: maximum likelihood via the Kalman filter, EM algorithm for hyperparameters, diffuse/augmented initialization, square-root/steady-state filters, Kalman smoother (RTS/disturbance), signal extraction, one-step-ahead prediction intervals, and smoothed state uncertainty bands. I provide residual diagnostics (standardized innovations, Ljung–Box), forecast evaluation, and cross-validation.
Extensions: time-varying parameters, stochastic volatility blocks, multivariate systems, exogenous regressors, regime switching, and structural decompositions (trend/seasonal/irregular). I work fluently with R packages such as KFAS, dlm, MARSS, FKF, and bsts, and can tailor the specification to your dataset and research goals.
Deliverables: clean R scripts, clear figures, and a concise memo describing model equations, estimation, diagnostics, and interpretation. I’m very familiar with these methods and can provide hands-on R programming help for coursework, projects, and theses.
Get help: engagements start at USD $150; fixed quotes follow a quick review of your brief and data.